上海交通大学附属中学2019—2020学年高中二年级上学期期末考试数学卷

上海交通大学附属中学2019—2020学年高中二年级上学期期末考试数学卷

1、填空题

1．复数z满足i•z＝1．则Imz＝__________．

2．已知抛物线y＝4x2，则焦点的坐标为__________．

3．若z（i为虚数单位，a＞0），|z3|＝5，则a的值为__________．

4．直线（参数t∈R）的倾斜角为__________．

5．若方程（k﹣1）x2+（5﹣2k）y2＝1表示的曲线为双曲线，则实数k的取值范围为__________．

6．若双曲线的渐近线方程为y＝±3x，且过点A（1，），则双曲线的方程是__________．

7．点P为直线3x+4y+4＝0上的动点，点Q为圆C：x2+y2﹣2x﹣4y+4＝0上的动点，则|PQ|的最小值为__________．

8．已知F1、F2是椭圆C：1（a＞b＞0）的两个焦点，P为椭圆C上的一点，且⊥，若△PF1F2的面积为4，则b＝__________．

9．已知a，b∈R+，若直线x+2y+3＝0与直线（a﹣1）x+by＝2互相垂直，则ab的最大值等于__________．

10．已知曲线Γ：，（θ∈[0，]）上一动点P，曲线Γ与直线x＝1交于点Q．则•的最大值是__________．

11．在平面直角坐标系xOy中，设定点A（a，a），P是函数y（x＞0）图象上一动点，若点P，A之间的最短距离为2，则满足条件的实数a的所有值为__________．

12．已知椭圆Γ：1和圆O：x2+y2＝r2（r＞0），设点A为椭圆Γ上的任一点，过A作圆O的两条切线，分别交椭圆Γ于B，C两点，若直线BC与圆O相切，则r＝__________．

2、选择题

13．设z为非零复数，则“z∈R“是|z|＝1”的（）

A．充分非必要条件 B．必要非充分条件

C．充要条件 D．既非充分也非必要条件

14．如图，与复平面中的阴影部分（含边界）对应的复数集合是（）

A． B．

C． D．

15．过抛物线y2＝4x的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于2，则如此的直线（）

A．有且仅有一条 B．有且仅有两条

C．有无穷多条 D．没有

16．曲线Γ：（1）0，要使直线y＝m（m∈R）与曲线Γ有四个不一样的交点，则实数m的取值范围是（）

A．（，）

B．（﹣3，3）

C．（﹣3，）∪（，3）

D．（﹣3，）∪（，）∪（，3）

3、解答卷

17．已知实系数一元二次方程x2+ax+b＝0（a，b∈R）的一根为﹣2i（i为虚数单位），另一根为复数z．

（1）求复数z，与实数a，b的值；

（2）设复数z的一个平方根为λ，记λ、λ2、λ﹣λ2在复平面上对应点分别为A、B、C，求（）•的值．

18．如图，某野生保护区监测中心设置在点O处，正西、正东、正北处有三个监测点A、B、C，且|OA|＝|OB|＝|OC|＝30km，一名野生动物察看员在保护区遇险，发出求教信号，三个监测点均收到求救信号，A点接收到信号的时间比B点接收到信号的时间早秒（注：信号每秒传播V0千米）．

（1）以O为原点，直线AB为x轴打造平面直角坐标系（如题），依据题设条件求察看员所大概出现的地方的轨迹方程：

（2）若已知C点与A点接收到信号的时间相同，求察看员遇险地址坐标，与与监测中心O的距离：

（3）若C点监测点信号失灵，现立即以监测点C为圆心进行“圆形”红外扫描，为保证有救援期望，扫描半径r至少是多少公里？

19．已知椭圆Γ：，过点D（﹣1，0）的直线l：y＝k（x+1）与椭圆Γ交于M、N两点（M点在N点的右边），与y轴交于点E．

（1）当m＝1且k＝1时，求点M、N的坐标；

（2）当m＝2时，设，，求证：λ+μ为定值，并求出该值；

20．设抛物线Γ：y2＝2px（p＞0），D（x0，y0）满足y02＞2px0，过点D作抛物线Γ的切线，切点分别为A（x1，y1），B（x2．y2）．

（1）求证：直线yy1＝p（x+x1）与抛物线Γ相切：

（2）若点A坐标为（4，4），点D在抛物线Γ的准线上，求点B的坐标：

（3）设点D在直线x+p＝0上运动，直线AB是不是恒过定点？若恒过定点，求出定点坐标：若没有，请说明理由．

21．已知椭圆Ω：1．双曲线Γ的实轴顶点就是椭圆Ω的焦点，双曲线Γ的焦距等于椭圆Ω的长轴长．

（1）求双曲线Γ的规范方程；

（2）设直线1经过点E（3，0）与椭圆Ω交于A、B两点，求△OAB的面积的最大值；

（3）设直线1：y＝kx+m（其中k，m为整数）与椭圆Ω交于不同两点A、B，与双曲线Γ交于不同两点C、D，问是不是存在直线l，使得向量，若存在，指出如此的直线有多少条？若存在，请说明理由．

1、填空题

1．【解析详解】由i•z＝1，得z，

∴Imz＝﹣1．

故答案为：﹣1．

2．【解析详解】抛物线y＝4x2的规范方程为x2y，焦点在y轴的正半轴上，p，，

 故焦点坐标为（0，），

故答案为：（0，）．

3．【解析详解】z2a﹣i，

由|z3|＝5，得，

即4a2+1＝5，得a＝1（a＞0）．

故答案为：
1．

4．【解析详解】直线（参数t∈R）转换为直角坐标方程为：x﹣2y＝2﹣6，即x﹣2y+4＝0，

故直线的斜率为k，

所以直线的倾斜角为．

故答案为：

5．【解析详解】方程（k﹣1）x2+（5﹣2k）y2＝1表示的曲线为双曲线，

可得（k﹣1）•（5﹣2k）＜0，解得k＜1或k．

故答案为：（﹣∞，1）∪（，+∞）．

6．【解析详解】由题意可知，可设双曲线的方程是x2k，把点（1，）代入方程解得 k，

故所求的双曲线的方程是y2﹣9x2＝1，

故答案为：y2﹣9x2＝1．

7．【解析详解】由圆的规范方程（x﹣1）2+（y﹣2）2＝1得圆心坐标为C（1，2），半径R＝1，

圆心到直线的距离d3，

在|PQ|的最小值为d﹣R＝2；

故答案为：2

8．【解析详解】∵F1、F2是椭圆C：1（a＞b＞0）的两个焦点，

P为椭圆C上一点，且PF1⊥PF2，

∴|PF1|+|PF2|＝2a，

|PF1|2+|PF2|2＝4c2，|PF1|•|PF2|＝4，

∴（|PF1|+|PF2|）2＝4c2+2|PF1||PF2|＝4a2，

∴16＝4（a2﹣c2）＝4b2，

∴b＝2．

故答案为：2．

9．【解析详解】依据题意，若直线x+2y+3＝0与直线（a﹣1）x+by＝2互相垂直，

则有（a﹣1）+2b＝0，变形可得a+2b＝1，

则ab（a×2b）（）2，当且仅当a＝2b时，等号成立；

即ab的最大值为，

故答案为：．

10．【解析详解】曲线Γ：，（θ∈[0，]）上一动点P，曲线Γ与直线x＝1交于点Q．

2cosplayθ＝1⇒cosplayθ⇒θ；

∴sin；

即Q（1，）；

∴•（2cosplayθ，sinθ）•（1，）＝2cosplayθsinθsin（θ+φ）；tanφ；φ∈（0，）；

∴θ+φ∈（φ，φ）；

∴θ+φ时，•取最大值且最大值为；

故答案为：

11．【解析详解】设点P，则|PA|，

令，∵x＞0，∴t≥2，

令g（t）＝t2﹣2at+2a2﹣2＝（t﹣a）2+a2﹣2，

①当a≤2时，t＝2时g（t）获得最小值g（2）＝2﹣4a+2a2，解得a＝﹣1；

②当a＞2时，g（t）在区间[2，a）上单调递减，在（a，+∞）单调递增，∴t＝a，g（t）获得最小值g（a）＝

a2﹣2，∴a2﹣2，解得a．

综上可知：a＝﹣1或．

故答案为﹣1或．

12．【解析详解】可以取A为椭圆左顶点，则A（﹣3，0），

BC方程为x＝r，代入椭圆Γ：1，得y．

设B（r，），则AB的方程为：，

整理得：．

由，得（5r﹣6）（r3+12r2+45r+54）＝0，

则r．

故答案为：．

2、选择题

13．【解析详解】设z＝x+yi（x，y∈R，不同时为0），则zx+yixy（1）i∈R，∴y（1）＝0，∴y＝0，x≠0；或x2+y2＝1即|z|＝1．

∴“z∈R“是|z|＝1”的必要不充分条件．

故选：B．

14．【解析详解】由图形可知，满足条件的复数在单位圆内（含边界），

且复数对应点的纵坐标大于或等于，

故有|z|≤1，Imz，

故选：D．

15．【解析详解】过抛物线y2＝4x的焦点作一条直线与抛物线相交于A、B两点，

若直线AB的斜率没有，则横坐标之和等于2，合适．

故设直线AB的斜率为k，则直线AB方程为y＝k（x﹣1）

代入抛物线y2＝4x得，k2x2﹣2（k2+2）x+k2＝0

∵A、B两点的横坐标之和等于2，

∴，

∴方程无解，

∴如此的直线没有．

故选：A．

16．【解析详解】曲线Γ：（1）0，可知x，y∈[﹣3，3]，

图形如图：是一个圆与双曲线的一部分，由，解得y＝±，

曲线Γ：（1）0，

要使直线y＝m（m∈R）与曲线Γ有四个不一样的交点，可得m∈（﹣3，）∪（，3）．

故选：C．

3、解答卷

17．【解析详解】（1）由实系数的一元二次方程两根互为共轭复数，得z＝2i；

借助根与系数的关系，得a＝﹣2i+2i＝0，b＝﹣2i•2i＝4；

（2）复数z＝2i，则λ2＝2i；

设λ＝x+yi，x、y∈R；

所以x2﹣y2+2xyi＝2i，

即，解得x＝y＝1或x＝y＝﹣1；

所以λ＝1+i，或λ＝﹣1﹣i；

当λ＝1+i时，λ2＝2i，λ﹣λ2＝1﹣i；

所以A（1，1），B（0，2），C（1，﹣1），

所以（）•（1，3）•（1，﹣1）＝1﹣3＝﹣2；

当λ＝﹣1﹣i时，λ2＝2i，λ﹣λ2＝﹣1﹣3i，

所以A（﹣1，﹣1），B（0，2），C（﹣1，﹣3），

所以（）•（﹣1，1）•（﹣1，﹣3）＝1﹣3＝﹣2；

综上知，（）•的值为﹣2．

18．【解析详解】（1）以O为原点，直线AB为x轴打造平面直角坐标系，A点接收到信号的时间比B点接收到信号的时间早秒，

可知野生动物察看员在保护区遇险，发出求教信号的地方，在以AB为焦点的双曲线的左支，

所以c＝30，2a＝40，所以a＝20，则b＝10，

所以察看员所大概出现的地方的轨迹方程：1，x≤0．

（2）已知C点与A点接收到信号的时间相同，则察看员遇险地址既在双曲线上，又在y＝﹣x（x＜0）上，

所以，可得x＝﹣10，y＝10，

察看员遇险地址坐标（﹣10，10），

察看员遇险地址与监测中心O的距离：20．

（3）由题意可得以监测点C为圆心进行“圆形”红外扫描，可得x2+（y﹣30）2＝r2，与1，x≤0．

联立，消去x可得：9y2﹣300y+6500﹣5r2≥0，△＝90000﹣36（6500﹣5r2）≥0，解得r≥20．

为保证有救援期望，扫描半径r至少是20公里．

19．【解析详解】（1）当m＝1且k＝1时，椭圆Γ方程为：，直线l方程为：y＝x+1，

联立方程，消去y得：3x2+4x＝0，

解得：x＝0或，

∵M点在N点的右边，

∴M（0，1），N（，）；

（2）当m＝2时，椭圆Γ方程为：，

联立方程，消去y得：（2+3k2）x2+6k2x+3k2﹣6＝0，

设点M（x1，y1），N（x2，y2），

∴，

∵E（0，k），D（﹣1，0），

∴，

又∵，，

∴x1＝λ（x1+1），x2＝μ（x2+1），

∴，

∴λ+μ，

故λ+μ为定值3．

20．【解析详解】（1）由办法1、抛物线Γ：y2＝2px（p＞0），求导，2yy′＝2p，即，

所以在A（x1，y1）点的切线的斜率，

所以切线方程为，由y12＝2px1，整理得yy1＝p（x+x1），

所以直线yy1＝p（x+x1）与抛物线Γ相切；

办法2、由题意可知，，消去x，整理得y2﹣2y1y+2px1＝0，

则，

所以直线yy1＝p（x+x1）与抛物线Γ相切；

（2）办法1、由A（4，4）在抛物线上，则抛物线的方程y2＝4x，

由D在抛物线的准线上，所以直线AB过抛物线的焦点F（1，0），

所以x1x21，y1y2＝﹣1，所以x2，y2＝﹣1，

所以B（，﹣1）；

办法2、由A（4，4）在抛物线上，则抛物线的方程y2＝4x，

由（1）可知，直线AD的方程4y＝2（x+4），即y（x+4），则D（﹣1，），

直线BD的方程yy2＝p（x+x2），所以，

解得，所以B（，﹣1）；

（3）AB恒过定点（p，0），理由如下：

办法1、设D（﹣p，y0），由（1）可知直线AD的方程为，即直线BD的方程，

将D（﹣p，y0）代入切线方程，，

所以y1，y2是方程的两根，所以y1+y2＝2y0，y1y2＝﹣2p2．

直线AB的斜率，直线AB的方程x﹣x1（y﹣y1），

即，所以直线AB恒过定点（p，0）．

办法2、设D（﹣p，y0），

由抛物线的极点极线的性质，可知直线AB的方程为yy0＝p（x﹣p），所以直线AB恒过定点（p，0）．

21．【解析详解】（1）椭圆的焦点坐标为（±2，0），长轴长为8，设双曲线的方程，

则a＝2，c＝4，则b2＝12，双曲线的方程；

（2）由题意可知过点M的直线斜率存在且不等于0，设直线l方程为x＝my+3，A（x1，y1），B（x2，y2），

联立方程组，消去x，得（3m2+4）y2+18my﹣21＝0，

y1+y2，y1y2，

所以S△OAB|OE|×|y1﹣y2|33×46，

令12m2+7＝t≥7，则，

所以，

当且仅当t＝9，即时，取等号，

则S△OAB＝664，

所以△OAB面积的最大值为．

（3）存在这种直线y＝kx+m，使得向量成立，且如此的直线有9条．

由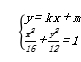，消去y，整理得（3+4k2）x2+8kmx+4m2﹣48＝0，

设A（x1，y1），B（x2，y2），

则x1+x2，△1＝（8km）2﹣4（3+4k2）（4m2﹣48）＞0，①

由，消去y，整理得（3﹣k2）x2﹣2kmx﹣m2﹣12＝0，

设C（x3，y4），D（x4，y4），

则x3+x4，△2＝（﹣2km）2+4（3﹣k2）（m2+12）＞0，②

由于，

所以（y4﹣y2）+（y3﹣y1）＝0．

由x1+x2＝x3+x4得．

所以2km＝0或．

由上式解得k＝0或m＝0．当k＝0时，

由①和②得﹣2m＜2．

由于m是整数，所以m的值为﹣3，﹣2，﹣1，0，1，2，3．

当m＝0，由①和②得k．

由于k是整数，所以k＝﹣1，0，1．

于是满足条件的直线共有9条．